Babak Keseluruhan

Scoreboard babak final Ngoding Seru 2019 dapat dilihat di sini.

Babak final Ngoding Seru 2019 diawali dengan soal Median Gabungan, yang dapat diselesaikan dengan observasi greedy sederhana dan mencari median untuk setiap subarray yang berukuran sama. Babak final Ngoding Seru 2019 diakhiri dengan soal Tempat Bersejarah, yang merupakan soal geometri pertama sekaligus soal tersulit pada Ngoding Seru 2019. Pada akhirnya, tidak terdapat finalis yang dapat menyelesaikan satu subsoal pun dari soal ini.

Seperti ditulis pada pengumuman sebelumnya, soal babak final Ngoding Seru 2019 sudah dapat Anda coba kembali di TLX Training Gate. Selamat kepada seluruh pemenang.

Credits:

  • Median Gabungan: Ditulis dan disiapkan oleh Muhammad Ayaz Dzulfikar.
  • Perjalanan Aritmetika: Ditulis dan disiapkan oleh Jonathan Irvin Gunawan.
  • Daun Terdekat: Ditulis dan disiapkan oleh Jonathan Irvin Gunawan.
  • Mengikuti Olimpiade: Ditulis oleh Jonathan Irvin Gunawan dan disiapkan oleh Muhammad Ayaz Dzulfikar.
  • Permainan Poin: Ditulis dan disiapkan oleh Wiwit Rifa'i.
  • Tempat Bersejarah: Ditulis dan disiapkan oleh Wiwit Rifa'i.
Solusi dan persiapan komponen soal lainnya dan juga review oleh Ashar Fuadi, Jonathan Irvin Gunawan, Muhammad Ayaz Dzulfikar, Sergio Vieri, dan Wiwit Rifa'i.
Penulis analisis:

Median Gabungan

Subsoal 1

Perhatikan bahwa median gabungan maksimum dapat dicapai apabila median favorit dari array A, B, dan C semaksimum mungkin. Sehingga, solusi dari permasalahan ini adalah mencari median favorit maksimum dari masing-masing array, lalu mencari median dari ketiga nilai tersebut.

Untuk subsoal 1, berhubung nilai N tidak terlalu besar, median favorit maksimum dapat dicari dengan menghitung median di masing-masing subarray yang berukuran K. Hal ini dapat dicapai dengan mengurutkan subarray tersebut, sehingga kompleksitas akhir adalah O(N × K × log K). Anda juga dapat menggunakan Quickselect (atau nth_element pada C++) untuk mencari elemen terkecil ke-x dari suatu array berukuran K dalam O(K). Dengan menggunakan cara ini, kompleksitas akhir adalah O(N × K).

Subsoal 2

Terdapat beberapa solusi untuk mencari median favorit maksimum dalam waktu lebih cepat dari O(N), seperti online median finding dan binary search. Yang akan dijelaskan di editorial ini adalah solusi yang menggunakan binary search.

Definisikan f(a, x) sebagai fungsi yang akan mengembalikan true apabila terdapat suatu subarray berukuran K dari array a dengan median yang tidak kurang dari x dan false apabila tidak ada. Fungsi ini dapat diimplementasikan dalam O(N). Pertama, definisikan array b dengan b[i] = 1 apabila a[i] ≥ x, dan b[i] = 0 apabila tidak. Maka, f(a, x) bernilai true jika terdapat subarray berukuran K pada b yang jumlahannya ≥ (K+1) / 2.

Maka, mencari median favorit maksimum dari suatu array dapat dilakukan dengan mencari x terbesar yang mana f(a, x) masih bernilai true. Hal ini dapat dilakukan dengan menggunakan binary search. Sehingga, kompleksitas akhir solusi ini adalah O(N × log N).

Perjalanan Aritmetika

Pertama, anggap bahwa jalan-jalan yang ada merupakan jalan satu arah yaitu dari kota dengan ketinggian yang lebih rendah ke kota dengan ketinggian yang lebih tinggi. Jika kedua kota memiliki ketinggian yang sama, kita dapat mengabaikan jalan tersebut. Karena semua jalan selalu mengarah ke kota yang lebih tinggi, maka dapat dijamin bahwa graf yang terbentuk dari susunan jalan tersebut membentuk sebuah directed acyclic graph (DAG). Oleh karena itu, kita dapat menggunakan dynamic programming (DP) pada graf ini. Kedua subsoal dalam soal ini dapat diselesaikan dengan DP, namun yang membedakan adalah seberapa efektif representasi dan proses perhitungan yang digunakan.

Subsoal 1

Definisikan fungsi f(u, v) sebagai banyaknya kota maksimum yang dapat dilewati dengan kota v adalah kota terakhir yang dicapai dan kota u adalah kota yang dilewati sebelum kota v. Untuk menghitung fungsi ini, kita dapat mengiterasi semua jalan yang mengarah ke kota u, lalu mengecek apakah kemiringannya sama dengan Hv - Hu. Jika tidak ada yang cocok, maka f(u, v) = 2. Namun jika ada, maka di antara jalan dengan kemiringan yang cocok tersebut, pilihlah jalur sehingga fungsi f(u, v) semaksimal mungkin.

Banyaknya total state yang perlu diperhatikan dalam fungsi tersebut hanyalah O(M) karena kita hanya perlu memperhatikan pasangan kota (u, v) sehingga terdapat jalan langsung dari u ke v. Namun, untuk menghitung setiap fungsi tersebut kita perlu mengiterasi jalan yang terhubung ke kota u, sehingga kasus terburuknya membutuhkan kompleksitas waktu O(M2).

Jadi, kompleksitas solusi ini adalah O(M2).

Subsoal 2

Untuk menyelesaikan subsoal ini, kita dapat melakukan optimasi dari solusi pada subsoal 1. Definisikan fungsi g(v, k) sebagai banyaknya kota maksimum yang dapat dilewati dengan hanya melewati jalan dengan kemiringan k dan kota terakhir yang dicapai adalah kota v. Sekilas kemiringan k mungkin saja sangat banyak kemungkinannya, namun kita dapat hanya memperhatikan kemiringan k sehingga terdapat jalan dari atau ke kota v dengan kemiringan k. Dengan kata lain, jika tidak ada jalan dengan kemiringan k yang terhubung dengan kota v, kita dapat mengabaikannya. Sehingga, secara keseluruhan state yang perlu diperhatikan adalah sebanyak O(M) sebab setiap jalan paling banyak akan menambah kemiringan baru pada 2 kota yang dihubungkannya.

Lalu, untuk menghitung fungsi g(v, k) kita hanya perlu mengiterasi jalan dengan kemiringan k yang menuju kota v. Jika tidak ada jalan yang memenuhi, maka kita dapat anggap g(v, k) = 1. Jika ternyata ada, pilihlah jalur yang memaksimalkan g(v, k). Perhatikan bahwa setiap jalan yang menghubungkan dari kota u ke kota v dengan kemiringan k, hanya akan digunakan sekali untuk menghitung g(v, k) berdasarkan g(u, k). Oleh karena itu, semua fungsi tersebut juga dapat dihitung dalam komplekstias waktu O(M).

Jadi, kompleksitas solusi ini adalah O(M).

Daun Terdekat

Kita dapat mendefinisikan d(x) untuk setiap node x sebagai jarak node x dan node 1. Untuk pertanyaan ke-i, kita dapat mencari daun x (Li ≤ x ≤ Ri) yang merupakan keturunan node Ui dan memiliki d(x) minimum. Jawaban dari pertanyaan tersebut adalah d(x) - d(Ui).

Subsoal 1

Subsoal ini dapat diselesaikan dengan menomori ulang seluruh node secara preorder sehingga seluruh node pada sebuah subpohon memiliki nomor-nomor node yang berurutan. Mari kita anggap pre(x) untuk setiap node x sebagai indeks kemunculan node x pada urutan preorder.

Kita juga dapat menggunakan sebuah struktur data mirip array. Jika node x adalah daun, maka elemen ke-pre(x) pada struktur data adalah d(x). Jika node x bukan merupakan daun, maka elemen ke-pre(x) pada struktur data adalah ∞. Jika terdapat pertanyaan dengan L = 1 dan R = N, maka kita dapat mencari nilai minimum pada struktur data pada indeks-indeks dari node-node yang merupakan keturunan node U. Karena indeks-indeks ini akan berurutan, struktur data Segment Tree dapat digunakan.

Karena R mungkin saja kurang dari N, pada awalnya kita dapat menginisialisasi struktur data dengan nilai ∞ untuk semua indeks. Berikutnya, kita dapat melakukan algoritma berikut: 

  inisialisasi DS dengan nilai ∞ untuk semua indeks
  for i ← 1 to N
    val ← d(i)
    if node i bukan daun:
      val ← ∞
    perbarui DS pada indeks pre(i) menjadi val
    jawab seluruh pertanyaan yang memiliki R = i menggunakan nilai DS saat ini

Kompleksitas waktu solusi ini adalah O((N + Q) × log(N)).

Subsoal 2

Subsoal ini dapat diselesaikan dengan menyimpan sebuah segment tree untuk setiap node. Pada node x, nilai pada indeks ke-y pada segment tree adalah d(y) jika node y merupakan daun dan keturunan node x, atau ∞ jika tidak. Dengan demikian, pertanyaan ke-i dapat dijawab dengan mencari nilai minimum di antara indeks Li dan Ri pada segment tree di node Ui.

Menyimpan segment tree pada seluruh node menghabiskan total waktu O(N2). Karenanya, untuk setiap node x, kita harus memanfaatkan segment tree pada anak-anak node x. Dari seluruh segment tree pada anak-anak node x, kita dapat menggunakan segment tree yang memiliki paling banyak elemen kurang dari ∞ sebagai nilai awal segment tree node x, dan "gabungkan" seluruh segment tree lainnya ke segment tree ini. Ketika kita sudah memiliki segment tree node x, kita dapat menjawab seluruh pertanyaan yang memiliki U = x.

Kompleksitas waktu solusi ini adalah O(N × log2(N)). Anda dapat membaca diskusi mengenai teknik ini dan kompleksitasnya pada blog post "Complexity of Merging Subsets on Trees" pada Codeforces.

Mengikuti Olimpiade

Subsoal 1

Pada awalnya kita dapat mengurutkan nilai S agar Si ≥ Si + 1 untuk semua 1 ≤ i < N. Kita ingin mencari nilai T1, T2, ..., TN sedemikian sehingga Ti > Ti + 1 untuk semua 1 ≤ i < N dan nilai |S1 - T1| + |S2 - T2| + ... + |SN - TN| seminimum mungkin.

Perhatikan bahwa syarat Ti > Ti + 1 untuk semua 1 ≤ i < N ekuivalen dengan Ti + i ≥ Ti + 1 + (i + 1) untuk semua 1 ≤ i < N. Karenanya, persoalan ini ekuivalen dengan mencari nilai T'1, T'2, ..., T'N sedemikian sehingga T'i ≥ T'i + 1 untuk semua 1 ≤ i < N dan nilai |S'1 - T'1| + |S'2 - T'2| + ... + |S'N - T'N| seminimum mungkin dengan S'i = Si + i untuk semua 1 ≤ i ≤ N.

Persoalan ini dapat diselesaikan dalam O(N2) menggunakan Dynamic Programming. Mari kita definisikan fi(j) sebagai nilai minimum |S'1 - T'1| + |S'2 - T'2| + ... + |S'i - T'i| dengan T'1 ≥ T'2 ≥ ... ≥ T'i ≥ j. Sehingga, f1(j) = min(k ≥ j) |k - S'1| dan fi(j) = min(k ≥ j) (fi - 1(k) + |k - S'i|) untuk semua 1 < i ≤ N.

Perhatikan bahwa fi(j) ≤ fi(j + 1). Definisikan nilai Opt(i) sebagai posisi yang meminimumkan fi. Dengan kata lain, Opt(i) adalah nilai terbesar yang memenuhi fi(Opt(i)) = fi(-∞). Opt(i) dapat dihitung dalam O(log (N)) dengan memperhatikan nilai S'i dan hanya menyimpan nilai-nilai k yang memenuhi fi(k) < fi(k + 1). Dengan demikian, terdapat solusi O(N × log(N)) untuk menyelesaikan persoalan ini. Detil solusi dapat dilihat pada blog post "Slope Trick" pada Codeforces.

Jika kita telah mendapatkan salah satu nilai optimal T' pada persoalan ini, maka nilai T dengan Ti = T'i - i untuk semua 1 ≤ i ≤ N merupakan salah satu nilai optimal pada persoalan awal. Kompleksitas waktu solusi ini adalah O(N × log(N)).

Subsoal 2

Syarat nilai T berbeda pada subsoal ini. Mari kita sebut indeks i sebagai indeks penting jika i muncul dalam O. Maka, syarat nilai T adalah Ti > Ti + 1 untuk seluruh indeks penting i dan Ti ≥ Ti + 1 untuk seluruh indeks non-penting i.

Perhatikan bahwa syarat ini ekuivalen dengan Ti + p(i) ≥ Ti + 1 + p(i + 1) untuk semua 1 ≤ i < N, dengan p(x) adalah banyaknya indeks penting yang tidak lebih dari x. Sehingga, kita dapat mendefinisikan S'i = Si + p(i) untuk semua 1 ≤ i ≤ N dan menggunakan solusi serupa dengan subsoal sebelumnya.

Kompleksitas waktu solusi ini juga adalah O(N × log(N)).

Permainan Poin

Subsoal 1

Subsoal ini dapat diselesaikan menggunakan dynamic programming. Mari kita definisikan fungsi f(r, c, k) (1 ≤ r ≤ R, 1 ≤ c ≤ C, 0 ≤ k ≤ K) sebagai banyaknya konfigurasi papan permainan menarik yang berukuran r baris c kolom dan dengan tepat k buah poin.

f(r, c, k) dapat dihitung secara rekursif dengan menjumlahkan beberapa kasus berdasarkan posisi posisi poin terakhir (yang memiliki indeks baris dan kolom terbesar) diletakkan (yaitu harus diletakkan pada baris ≤ r dan kolom ≤ c, namun tidak boleh tepat pada petak (r, c)).

  • Jika poin terakhir tidak terletak pada baris ke-r, maka banyaknya konfigurasi ini adalah f(r-1, c, k) + f(r-1, c, k-1). Kita perlu menambahkan f(r-1, c, k-1) karena f(r-1, c, k) tidak mencakup konfigurasi ketika poin terakhir diletakkan pada petak (r-1, c) dan jika kita meletakkan poin terakhir pada petak (r-1, c) maka sisa k-1 poin tersebut dapat disusun seperti pada f(r-1, c, k-1).
  • Dengan cara serupa dengan kasus sebelumnya, jika poin terakhir tidak terletak pada kolom ke-c, maka banyaknya konfigurasi ini adalah f(r, c-1, k) + f(r, c-1, k-1).
  • Dengan menggabungkan 2 kasus di atas, ketika poin terakhir tidak terletak di baris ke-r maupun di kolom ke-c, maka perhitungan tersebut menjadi terhitung 2 kali. Oleh karena itu, perlu dikurangi dengan f(r-1, c-1, k) + f(r-1, c-1, k-1).
Dengan kata lain, fungsi f(r, c, k) dapat dihitung secara rekursif sebagai f(r, c, k) = (f(r-1, c, k) + f(r-1, c, k-1)) + (f(r, c-1, k) + f(r, c-1, k-1)) - (f(r-1, c-1, k) + f(r-1, c-1, k-1)).

Basis dari fungsi ini adalah:

  • f(r, c, k) = 0, jika r < 1 atau c < 1 dan untuk semua 0 ≤ k ≤ K.
  • f(1, 1, k) = 0, untuk semua 0 ≤ k ≤ K.
  • f(r, c, 0) = 1, untuk semua 1 ≤ r ≤ R dan 1 ≤ c ≤ C selain dari 2 kasus di atas.

Jawaban yang diminta adalah f(R, C, K). Kompleksitas waktu solusi ini adalah O(R × C × K).

Subsoal 2

Misalkan petak-petak yang berisi poin adalah petak-petak (X1, Y1), (X2, Y2), ..., (XK, YK) dengan 1 ≤ X1 ≤ X2 ≤ ... ≤ XK ≤ R dan 1 ≤ Y1 ≤ Y2 ≤ ... ≤ YK ≤ C. Untuk memudahkan penjelasan, anggap bahwa (X0, Y0) = (1, 1) dan (XK + 1, YK + 1) = (R, C). Untuk semua 0 ≤ i ≤ K juga berlaku Xi < Xi + 1 atau Yi < Yi + 1.

Misalkan juga ΔXi = Xi + 1 - Xi dan ΔYi = Yi + 1 - Yi untuk semua 0 ≤ i ≤ K, maka kita dapatkan ΔX0 + ΔX1 + ... + ΔXK = R - 1 dengan ΔXi ≥ 0 untuk semua 0 ≤ i ≤ K dan ΔY0 + ΔY1 + ... + ΔYK = C - 1 dengan ΔYi ≥ 0 untuk semua 0 ≤ i ≤ K. Banyaknya barisan ΔX0, ΔX1, ..., ΔXK yang memenuhi persamaan tersebut dapat dihitung seperti persoalan stars and bars yaitu ada sebanyak C(R - 1 + K, K). Begitu juga dengan banyaknya barisan ΔY0, ΔY1, ..., ΔYK yang memenuhi persamaan tersebut ada sebanyak C(C - 1 + K, K).

Namun, jika kita mengalikan kedua rumus tersebut ada kemungkinan bahwa terdapat 0 ≤ i ≤ K sehingga ΔXi = 0 dan ΔYi = 0 yang bertentangan dengan syarat bahwa Xi < Xi + 1 atau Yi < Yi + 1 untuk semua 0 ≤ i ≤ K. Oleh karena itu, kita harus menghilangkan semua konfigurasi yang memiliki 0 ≤ i ≤ K sehingga ΔXi = 0 dan ΔYi = 0 dengan menggunakan prinsip inklusi-eksklusi.

Misalkan untuk setiap 0 ≤ i ≤ K, Ai adalah himpunan konfigurasi sehingga ΔXi = 0 dan ΔYi = 0. Sehingga, banyaknya konfigurasi yang harus dihapus adalah |A0 ∪ A1 ∪ ... ∪ AK| = (|A0| + |A1| + ... + |AK|) - (|A0 ∩ A1| + ... + |AK - 1 ∩ AK|) + ... + (-1)K (|A0 ∩ A1 ∩ ... ∩ AK|).

Untuk setiap 1 ≤ N ≤ K, kita dapat menghitung ∑|Ai1 ∩ Ai2 ∩ ... AiN| untuk semua 0 ≤ i1 < i2 < ... < iN ≤ K dengan rumus C(K + 1, N) × C(R - 1 + K - N, K - N) × C(C - 1 + K - N, K - N). Pada rumus tersebut, C(K + 1, N) berasal dari banyaknya cara memilih barisan i1, i2, ..., iN sehingga pada posisi ij haruslah berlaku ΔXij = 0 dan ΔYij = 0 untuk semua 1 ≤ j ≤ N. Sedangkan, C(R - 1 + K - N, K - N) × C(C - 1 + K - N, K - N) berasal dari banyaknya cara untuk mengisi ΔXj dan ΔYj untuk semua 0 ≤ j ≤ K selain dari barisan i1, i2, ..., iN.

Sedangkan untuk |A0 ∩ A1 ∩ ... ∩ AK|, kita dapat mengabaikannya karena tidak mungkin semua ΔXi = 0 dan ΔYi = 0 untuk semua 0 ≤ i ≤ K sekaligus, sehingga haruslah |A0 ∩ A1 ∩ ... ∩ AK| = 0.

Secara keseluruhan, untuk menghitung jawaban akhir dengan rumus-rumus di atas dapat dihitung dalam kompleksitas O(K) dengan bantuan beberapa precompute dalam O(max(R, C) + K).

Tempat Bersejarah

Subsoal 1

Subsoal ini dapat diselesaikan dengan dynamic programming. Sebelumnya, urutkan titik-titik secara memutar (misalnya berdasarkan sudut yang dibentuk dari sumbu X positif). Anggap salah satu titik sebagai titik awal. Lalu, nomori semua titik berdasarkan urutan memutar dimulai dari titik awal secara berlawanan arah jarum jam. Lalu, definisikan f(k) sebagai banyaknya minimum titik yang diperlukan untuk menghubungkan titik awal hingga ke titik ke-k menggunakan titik-titik dengan indeks 1 sampai k. Maka, f(k) dapat dihitung dengan:

  • f(1) = 1.
  • f(k) = min(f(j) + 1) untuk semua j < k sehingga titik ke-j dan titik ke-k dapat dihubungkan secara langsung tanpa memotong lingkaran. Perlu diperhatikan juga bahwa titik ke-j yang dipilih haruslah terletak di sebelah kanan garis yang melewati titik pusat dan titik ke-k, agar menjamin hasil yang diberikan memutari lingkaran dalam satu arah yang tetap. Jika tidak ada j yang memenuhi maka anggap f(k) sebagai ∞ yang menunjukkan tidak valid.
Anggap juga bahwa titik ke-(N+1) adalah titik awal, sehingga banyaknya titik yang diperlukan untuk memutari lingkaran dimulai dari titik awal dan kembali ke titik awal tersebut adalah f(N+1). Lalu, coba semua kemungkinan titik awal yang mungkin, dan cari jawaban yang terkecil.

Kompleksitas waktu solusi ini adalah O(N3).

Subsoal 2

Untuk menyelesaikan subsoal ini, diperlukan beberapa observasi penting.

Observasi pertama adalah jika titik P terletak di dalam segitiga yang dibentuk dari titik Q dan kedua titik singgungnya pada lingkaran, maka jika titik P terpilih dalam solusi maka titik P selalu dapat digantikan oleh titik Q dalam solusi tersebut. Hal ini berlaku karena jika sebuah titik dapat dihubungkan dengan titik P tanpa memotong lingkaran maka titik tersebut juga pasti dapat dihubungkan dengan titik Q. Sebagai ilustrasi, perhatikan gambar berikut.

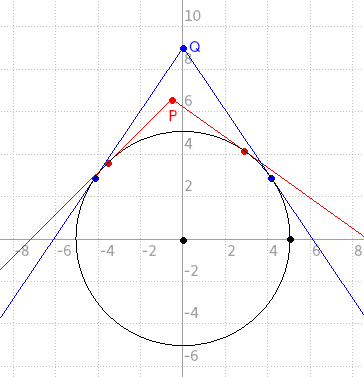
Sebut saja titik yang selalu dapat digantikan oleh titik lain sebagai titik yang tidak penting, sedangkan titik yang tidak dapat digantikan oleh titik lain sebagai titik penting. Karena kita dapat mengganti semua titik tidak penting dalam solusi dengan titik penting, maka kita dapat menghapus semua titik tidak penting.

Untuk mencari semua titik tidak penting, kita dapat menggunakan algoritma yang mirip dengan algoritma Graham Scan dalam mencari Convex Hull. Pertama, tandai semua titik sebagai titik penting. Lalu, iterasi titik-titik tersebut secara memutar sambil menyimpan sebuah stack yang berisi titik-titik yang masih dianggap penting. Awalnya, stack tersebut kosong. Ketika kita mengiterasi titik P, cek apakah titik terakhir di stack tersebut dapat digantikan oleh titik P. Jika iya, maka tandai titik tersebut sebagai tidak penting dan hapus dari stack. Lakukan hal tersebut berulang kali hingga stack tersebut kosong atau titik terakhir pada stack tidak lagi dapat digantikan oleh titik P. Lalu, cek juga apakah titik P dapat digantikan oleh titik terakhir pada stack, jika iya maka tandai titik P sebagai titik tidak penting, sedangkan jika tidak maka masukkan titik P ke dalam stack. Lakukan iterasi sebanyak 2 kali putaran agar menjamin semua titik tidak penting sudah ditandai dengan benar.

Sekarang, anggap bahwa semua titik yang tersisa adalah titik-titik penting. Observasi kedua adalah jika titik P, Q, dan R adalah titik-titik yang ketiganya tidak dapat saling menggantikan, dan posisi sudut Q di antara P dan R sehingga memenuhi ∠POQ + ∠QOR = ∠POR (dengan ∠ABC menyatakan nilai sudut terkecil yang dibentuk oleh segmen garis BA dan segmen garis BC) maka jika P dapat dihubungkan dengan R, akan berakibat Q juga dapat dihubungkan dengan P maupun R. Sebagai ilustrasi, perhatikan gambar berikut.

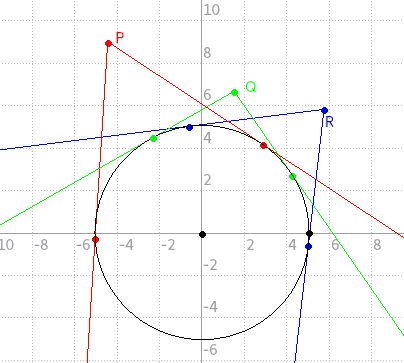
Berdasarkan observasi kedua, jika semua titik penting diurutkan secara memutar maka titik-titik penting yang dapat dihubungkan langsung oleh sebuah titik penting akan terletak pada posisi indeks yang bersebelahan dalam urutan tersebut. Oleh karena itu, kita dapat melakukan sebuah pendekatan greedy untuk mencari solusi pada titik-titik penting. Pertama, pilih salah satu titik sebagai titik awal dalam solusi. Lalu, dalam arah sudut tertentu pilih titik dengan sudut terjauh dalam arah tersebut yang masih dapat dihubungkan oleh titik terakhir yang dipilih dalam solusi. Lakukan hal tersebut, sampai memutari lingkaran dan kembali ke titik awal. Namun solusi ini memerlukan kompleksitas waktu O(N2) sebab kita harus mencoba semua kemungkinan titik awal.

Untuk mengoptimasi solusi greedy tersebut, kita dapat melakukan binary lifting sehingga untuk setiap titik awal yang dipilih hanya memerlukan kompleksitas waktu O(log(N)) untuk menghitung minimal titik yang dibutuhkan untuk memutari lingkaran dan kembali ke titik awal. Pertama, kita dapat melakukan precompute untuk mengetahui titik terjauh yang dapat dihubungkan dalam satu arah sudut tertentu dari seluruh titik. Lalu, definsikan g(i, P) adalah banyaknya titik yang dilewati setelah memilih 2i titik menggunakan pendekatan greedy di atas yang dimulai dari titik P. Tujuan kita adalah untuk melewati N titik yang berarti memutari lingkaran dan kembali ke titik awal. Untuk melakukan hal itu, kita dapat mencoba i dimulai dari ⌊2log(N)⌋ hingga 0, cek apakah jika menambah g(i, P) ke jumlah titik yang dilewati akan melebihi N atau belum. Jika belum, maka tambahkan 2i ke jumlah titik dalam solusi dan perbarui titik terakhir yang dipilih dalam solusi. Nilai-nilai g(i, P) dapat dihitung dalam precompute terlebih dahulu dalam O(N × log(N)).

Kompleksitas waktu solusi ini adalah O(N × log(N)).