Babak Keseluruhan
Scoreboard babak 2 Ngoding Seru 2019 sudah dicairkan (unfrozen).
Babak 2 Ngoding Seru 2019 diawali dengan soal Menghitung Password, yang merupakan soal kombinatorik sederhana. Berbeda dengan babak sebelumnya, kali ini Babak 2 berisi empat soal yang memiliki tingkat kesulitan lebih tinggi daripada soal-soal pada babak sebelumnya.
Seluruh peserta yang mendapatkan peringkat 20 besar pada babak ini dapat mengikuti babak final. Kami akan memastikan waktu kompetisi babak final dalam waktu 24 jam. Setelah kami sudah memastikan waktu kompetisi babak final, kami akan mengumumumkannya dan mengirimkan e-mail kepada seluruh 20 besar untuk konfirmasi kehadiran babak final.
Credits:
- Menghitung Password: Ditulis dan disiapkan oleh Jonathan Irvin Gunawan.
- Pembagian Tim: Ditulis dan disiapkan oleh Muhammad Ayaz Dzulfikar.
- Komunikasi Grup: Ditulis dan disiapkan oleh Muhammad Ayaz Dzulfikar.
- Memindahkan Mobil: Ditulis dan disiapkan oleh Wiwit Rifa'i.
Penulis analisis:
- Menghitung Password: Jonathan Irvin Gunawan.
- Pembagian Tim: Muhammad Ayaz Dzulfikar.
- Komunikasi Grup: Wiwit Rifa'i.
- Memindahkan Mobil: Wiwit Rifa'i.
Menghitung Password
Subsoal 1
Subsoal ini dapat diselesaikan dengan mencoba seluruh kemungkinan password yang mungkin. Terdapat MN kemungkinan password yang mungkin. Untuk setiap kemungkinan password, kita dapat menguji apakah tombol i ditekan pada detik ke-Ti untuk terakhir kalinya. Jika iya, kita dapat menambahkan satu pada variabel penghitung jawaban. Kompleksitas waktu solusi ini adalah O(MN × (M + N)).
Subsoal 2
Mari kita amati simbol ke-i pada password Felice. Jika sebuah simbol (katakan simbol j) ditekan pada detik ke-i untuk terakhir kalinya, maka hanya terdapat satu kemungkinan simbol yang mungkin sebagai simbol ke-i pada password Felice (yaitu simbol j). Jika tidak, maka banyaknya kemungkinan simbol yang mungkin sebagai simbol ke-i pada password Felice adalah banyaknya simbol yang muncul pada detik ke-(lebih dari i) untuk terakhir kalinya. Dengan kata lain, banyaknya kemungkinan simbol yang mungkin sebagai simbol ke-i pada password Felice adalah banyaknya indeks k yang memenuhi Tk > i.
Karena kemungkinan simbol yang mungkin sebagai simbol ke-i pada password Felice tidak bergantung pada simbol lainnya pada password Felice, kita dapat menggunakan hukum perkalian untuk menghitung banyaknya kemungkinan password Felice. Untuk menghitung kemungkinan simbol yang mungkin sebagai simbol ke-i (untuk semua i) secara efisien, kita dapat melakukan iterasi dari N sampai 1 dan menambahkan satu pada variabel penghitung simbol setiap kali terdapat simbol yang ditekan pada detik ke-i untuk terakhir kalinya.
Kompleksitas waktu solusi ini adalah O(M + N).
Pembagian Tim
Untuk kemudahan berdiskusi, definisikan kandidat tim ke-i sebagai kandidat tim dengan urutan ke-i apabila seluruh kandidat tim diurutkan berdasarkan cabang, lalu urutannya dalam cabang tersebut. Lalu, definisikan L sebagai jumlah semua Mi.
Subsoal 1
Ingat bahwa apabila suatu kandidat tim akan dimasukkan ke dalam tim yang ikut perlombaan, maka kita harus memilih salah satu anggotanya menjadi ketua tim. Berhubung banyaknya peserta pada subsoal ini sedikit, kita dapat mengerjakan subsoal ini dengan dynamic programming. Definisikan f(i, x) (1 ≤ i ≤ L, x subset dari {1, 2, ..., N}) sebagai banyak tim maksimum yang dapat diikutkan apabila kita hanya dapat menggunakan kandidat tim ke-1 sampai ke-i, dan peserta dalam daftar x tidak dapat menjadi ketua tim lagi. Maka, terdapat 2 rekurensi:
- Tidak mengikutsertakan tim ke-i. Artinya, coba f(i - 1, x).
- Mengikutsertakan tim ke-i. Artinya, coba satu per satu semua anggota kandidat tim ke-i yang belum menjadi ketua tim (misal sekarang mencoba y), dan coba f(i - 1, x ∪ {y}) + 1.
Kompleksitas solusi ini adalah O(2N × L).
Subsoal 2
Kita dapat merepresentasikan kandidat tim dan peserta dalam sebuah bipartite graph. Anggap himpunan node U sebagai kandidat tim (satu kandidat tim direpresentasikan oleh satu node), dan himpunan node V sebagai peserta (satu peserta direpresentasikan oleh satu node). Buat sebuah edge yang menghubungkan node kandidat tim dengan node peserta yang merupakan anggota kandidat tim tersebut. Sebagai contoh, berikut adalah representasi graf untuk contoh masukan:
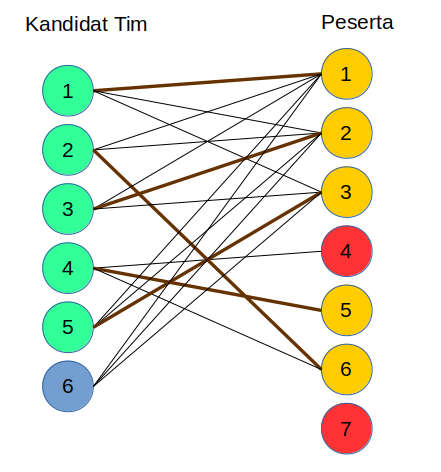
Garis tebal merepresentasikan siapa yang menjadi ketua untuk kandidat tim tersebut. Definisikan edge dengan garis tebal sebagai edge yang diambil.
Dalam representasi graf tersebut, memaksimalkan tim yang diikutkan sama saja dengan memaksimalkan banyaknya edge yang diambil, dengan syarat himpunan edge yang diambil tidak boleh memiliki ujung kandidat tim yang sama atau peserta yang sama. Ini sama dengan persoalan matching. Lebih spesifiknya, persoalan ini sama dengan mencari maximum cardinality bipartite matching (MCBM).
Mencari MCBM dapat dilakukan dalam O(V × E) dengan augmenting path. Karena V = L + N, dan E = 3 × L, maka kompleksitas solusi ini adalah O((L + N) × L).
Komunikasi Grup
Struktur dari pengiriman pesan oleh N orang pada soal membentuk sebuah struktur tree. Setiap node merepresentasikan orang, dan setiap edge menyatakan bahwa 2 orang yang dihubungkan oleh edge tersebut dapat saling mengirimkan pesan secara langsung. Kita dapat menganggap bahwa setiap node memiliki warna hitam atau putih. Jika seseorang merupakan anggota grup maka node orang tersebut akan berwarna hitam, dan akan berwarna putih jika orang tersebut bukan anggota grup. Biaya untuk mengadakan acara adalah jumlah dari jarak setiap 2 node yang berwarna hitam.
Untuk memudahkan pembahasan, kita dapat menganggap bahwa pada awalnya semua node berwarna putih, sehingga biaya untuk mengadakan acara adalah 0. Kemudian untuk setiap orang yang sebenarnya merupakan anggota sejak awal, kita ubah warna node tersebut menjadi hitam. Setiap kali kita mengubah warna sebuah node menjadi hitam, biaya untuk mengadakan acara akan bertambah sebanyak jumlah jarak dari node tersebut ke semua node hitam yang lain. Sedangkan ketika kita mengubah warna sebuah node menjadi putih, maka biaya untuk mengadakan acara akan berkurang sebanyak jumlah jarak dari node tersebut ke semua node hitam yang lain. Dengan begitu, pada setiap saat kita dapat mengetahui berapa biaya untuk mengadakan acara pada grup tersebut.
Sehingga, persoalan yang tersisa adalah setiap kali kita mengubah warna node, bagaimana caranya untuk menghitung jumlah jarak dari node tersebut ke semua node lain yang berwarna hitam.
Subsoal 1
Untuk menyelesaikan subsoal ini, kita dapat menggunakan Depth First Search (DFS) untuk mengiterasi semua node sambil menghitung jarak dari node yang akan diganti warnanya ke node yang sedang dilewati. Lalu, jumlahkan semua jarak node-node yang berwarna hitam. Karena setiap DFS akan berjalan dalam O(N) dan terdapat paling banyak O(N + Q) perubahan warna, kompleksitas solusi ini adalah O((N + Q) × N).
Subsoal 2
Untuk suatu konfigurasi warna pada tree, kita dapat menghitung jumlah jarak dari suatu node ke semua node hitam secara bersamaan untuk semua node dalam O(N). Kita dapat melakukan 2 kali DFS untuk menghitung nilai-nilai tersebut. DFS pertama dilakukan untuk menghitung jumlah jarak dari node hitam pada masing-masing subtreenya. Lalu, DFS kedua dilakukan untuk menambahkan jumlah jarak dari node hitam di luar subtreenya berdasarkan perhitungan dari DFS pertama. Nilai-nilai yang sudah dihitung tersebut akan digunakan sebagai precompute untuk mempercepat perhitungan jumlah jarak dari suatu node ke semua node hitam untuk memperbarui jawaban ketika terjadi perubahaan warna pada suatu node. Selain itu, kita juga perlu menyimpan sebuah list yang berisi node-node yang warnanya berbeda dengan sejak perhitungan precompute terakhir dilakukan.
Pada awalnya, lakukan perhitungan precompute tersebut pada konfigurasi warna awal dan gunakan juga nilai precompute tersebut untuk menghitung jawaban awal. Lalu, setiap kali kita ingin memperbarui jawaban karena terdapat perubahaan warna pada suatu node, kita dapat menggunakan nilai precompute yang terakhir kali dihitung dengan ditambahkan atau dikurangi jarak dari node tersebut ke node-node pada list. Jarak dua node pada tree dapat dihitung dengan mencari lowest common ancestor (LCA) kedua node tersebut, jika kita asumsikan salah satu node manapun pada tree sebagai root. LCA dapat dihitung dalam O(log(N)) atau O(1). Dengan begitu, jika kita dapat menjaga agar panjang list tidak lebih dari √Q, maka perhitungan jumlah jarak dari sebuah node ke semua node hitam dapat dihitung dalam O(√Q).
Kita dapat menjaga agar panjang list tidak lebih dari √Q yaitu setiap kali panjang list sudah lebih dari √Q, maka perhitungan precompute jumlah jarak dari setiap node ke semua node hitam perlu dilakukan ulang berdasarkan konfigurasi warna sekarang. Sehingga, list tersebut menjadi kosong kembali. Perhitungan ulang tersebut tidak akan dilakukan lebih dari Q/√Q = √Q kali, sehingga secara keseluruhan perhitungan ulang dapat dilakukan dalam O(N × √Q). Jadi, kompleksitas solusi ini adalah O((N + Q) × √Q).
Soal ini juga dapat diselesaikan dengan pendekatan Heavy Light Decomposition (dengan kompleksitas O(N log2(N)) atau Centroid Decomposition (dengan kompleksitas O(N log(N)). Namun, pendekatan tersebut tidak diperlukan untuk menyelesaikan soal ini dan tidak akan dijelaskan dalam pembahasan kali ini untuk diserahkan kepada pembaca sebagai latihan.
Memindahkan Mobil
Karena konfigurasi akhir yang diinginkan adalah seluruh mobil berwarna biru berada di sebelah kiri seluruh mobil berwarna kuning, maka kita bisa menganggap bahwa terdapat sebuah garis pemisah sehingga sebelah kiri garis tersebut hanya boleh diisi oleh mobil berwarna biru sedangkan sebelah kanan garis hanya untuk mobil berwarna kuning. Tentu saja, banyak petak parkir di sebelah kiri garis tidak boleh kurang dari banyaknya mobil biru, dan banyak petak parkir di sebelah kanan garis tidak boleh kurang dari banyaknya mobil kuning. Kita bisa mencoba semua kemungkinan garis pemisah yang mungkin.
Misalkan garis pemisah terletak di antara petak parkir ke-M dan ke-(M+1). Maka, semua mobil biru yang awalnya berada di sebelah kanan garis harus dipindahkan ke sebelah kiri garis dan mobil kuning yang awalnya berada di sebelah kiri garis harus dipindahkan ke sebelah kanan garis. Misalkan juga P adalah himpunan nomor petak dari mobil-mobil biru yang harus dipindahkan, dan Q adalah himpunan nomor petak dari mobil-mobil kuning yang harus dipindahkan. Energi terkecil yang mungkin dicapai untuk memindahkan mobil dari P dan Q tersebut adalah ketika kita dapat memindahkan mobil dari P ke sebelah kiri garis, namun dengan posisi sekanan mungkin dan mobil dari Q ke sebelah kanan garis yang sekiri mungkin. Dengan kata lain, misalkan X adalah himpunan dari |P| buah petak terkanan di sebelah kiri garis yang tidak ditempati oleh mobil biru, dan Y adalah himpunan dari |Q| buah petak terkiri di sebelah kanan garis yang tidak ditempati oleh mobil kuning, maka energi terkecil yang mungkin dapat dicapai dengan memindahkan mobil-mobil dari P ke X dan dari Q ke Y secara langsung tanpa memindahkan mobil ke petak lain untuk sementara. Tentu saja, jika P = Y dan Q = X, maka hal tersebut tidak mungkin dapat dilakukan sebab pada langkah pertama, kita tidak bisa memindahkan mobil ke petak di X atau Y karena tidak ada petak di X dan Y yang kosong. Lalu, bagaimana jika P ≠ Y atau Q ≠ X?
Ternyata, jika P ≠ Y atau Q ≠ X, maka kita pasti bisa memindahkan mobil-mobil dari P ke X dan dari Q ke Y. Without loss of generality, asumsikan bahwa Q ≠ X untuk mempermudah pembahasan. Hal tersebut berarti terdapat petak pada X yang kosong (tidak terisi oleh mobil kuning), sehingga pada langkah pertama kita bisa memindahkan mobil biru dari P ke petak kosong tersebut. Pilihlah mobil biru yang terkiri pada P. Setelah mobil tersebut dipindahkan, hapus petak awal dari P dan petak tujuan mobil tadi dari X. Perhatikan bahwa setiap kita berhasil memindahkan mobil dari petak terkiri P ke petak di X, maka pada langkah selanjutnya kita juga pasti bisa memindahkan mobil dari petak terkanan Q ke salah satu petak di Y. Sebab, petak terkiri Y pasti sama dengan petak terkiri P, atau berada di sebelah kiri petak terkiri P, dan karena mobil di petak terkiri P sudah berhasil dipindahkan berarti petak tersebut menjadi kosong dan dapat dipastikan bahwa petak terkiri Y juga kosong. Hal tersebut juga berlaku sebaliknya. Dengan melakukannya berulang-ulang secara bergantian, maka semua mobil dari petak di P dapat dipindahkan ke petak di X dan semua mobil dari petak di Q dapat dipindahkan ke petak di Y.
Lalu, jika ternyata P = Y dan Q = X, maka setelah langkah pertama apapun, kita pasti bisa melakukan strategi greedy yang sudah dijelaskan tadi. Jika pada langkah pertama, kita memindahkan mobil biru dari P ke kanan terlebih dahulu, atau memindahkan mobil kuning dari Q ke kiri terlebih dahulu, maka energi untuk jarak tersebut akan terhitung dua kali karena mobil tersebut nanti akan dipindahkan ke arah sebaliknya lagi, sehingga kurang efektif. Oleh karena itu, cukup menangani 2 buah kasus untuk langkah pertama tersebut, yaitu memindahkan salah satu mobil biru dari P ke petak kosong terkanan di sebelah kiri garis, atau memindahkan salah satu mobil kuning dari Q ke petak kosong terkiri di sebelah kanan garis. Dan terakhir, lakukan strategi greedy tadi.
Subsoal 1
Subsoal ini dapat diselesaikan dengan simulasi strategi tadi secara langsung untuk setiap garis pemisah yang mungkin dalam O(N). Karena terdapat kurang dari N buah garis pemisah yang mungkin, maka total kompleksitasnya menjadi O(N2).
Subsoal 2
Perhatikan bahwa energi total yang dihabiskan dalam strategi tadi untuk memindahkan mobil-mobil dari P ke X dan dari Q ke Y adalah sum(P) - sum(X) + sum(Y) - sum(Q). Nilai-nilai dari sum(P), sum(Q), sum(X), dan sum(Y) dapat dihitung secara cepat dengan menggunakan prefix sum. Lalu, untuk mencari batas-batas indeks agar |X| = |P| dan |Y| = |Q|, kita dapat menggunakan binary search dalam O(log(N)), atau batas indeks tersebut juga dapat dihitung dalam O(1) dengan bantuan lookup table. Karena harus mencoba O(N) buah garis pembatas yang mungkin, maka total kompleksitasnya adalah O(N × log (N)) atau bisa juga dalam O(N).